基于WPS的一阶常微分方程数值求解
1 研究问题
一阶微分方程初值问题
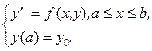 (1)
(1)
的数值解。
2 数值解法
设定步长为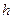 ,
,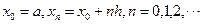 .
.
2.1欧拉法
2.1.1 欧拉公式
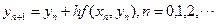 (2)
(2)
2.1.2 欧拉中点公式
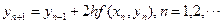 (3)
(3)
2.1.3 预估-校正法
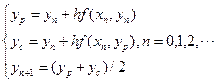 (4)
(4)
2.2 龙格-库塔法
四级四阶龙格库塔法
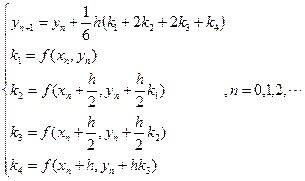 (5)
(5)
3 算例与WPS求解
假定方程为
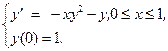 (6)
(6)
为检验算法有效性,先求解析解,再求数值解,便于比较。
3.1解析解
令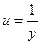 ,则
,则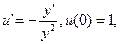 ,原方程可化为
,原方程可化为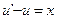 ,可用常数变易法或由一阶线性微分方程
,可用常数变易法或由一阶线性微分方程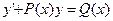 的公式
的公式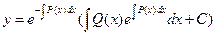 ,可得
,可得
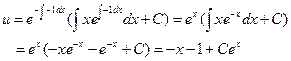 ,
,
再由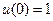 ,得
,得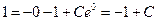 ,得
,得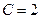 ,
,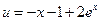 ,所以
,所以

3.2 数值求解的欧拉法
步骤1:新建表格文档
步骤2:根据步长设置自变量范围
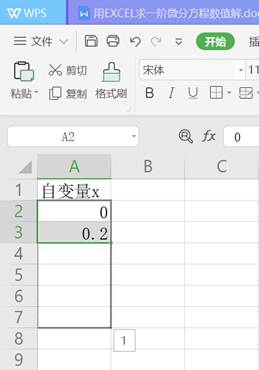
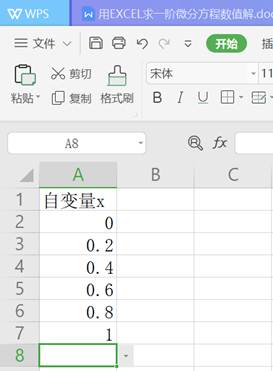
先在第一列第2到3行分别输入0,0.2,选中这两行,移动鼠标,出现“+”号是下拉。
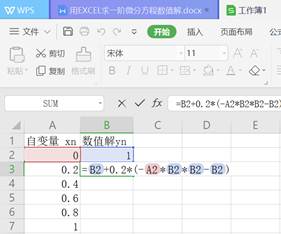
步骤3:在B2输入初值1,然后在B3输入欧拉公式,回车或打对号后,再选中往下拉。
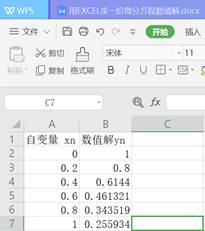
步骤4:求出解析解
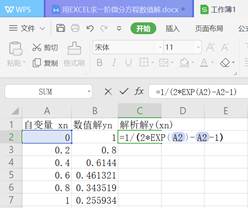

步骤5:绘图比较选中所有数据,插入散点图
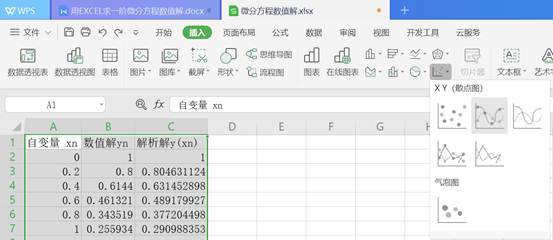
得到运行结果如下:
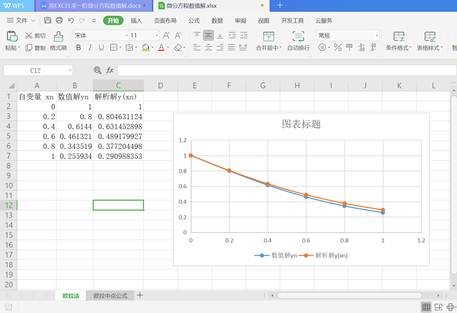
可以看到,随着x的增大,数值解逐渐偏离了解析解。
3.2 数值求解的欧拉中点法
类似的步骤,可得下图,可见得到很大改善,数值解与解析解几乎重合。
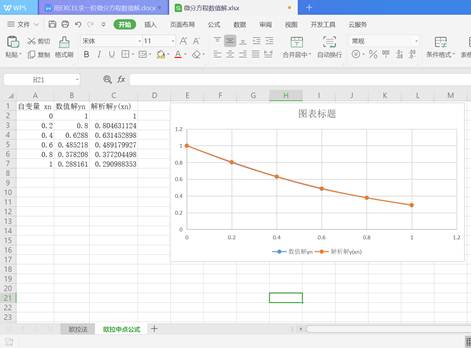
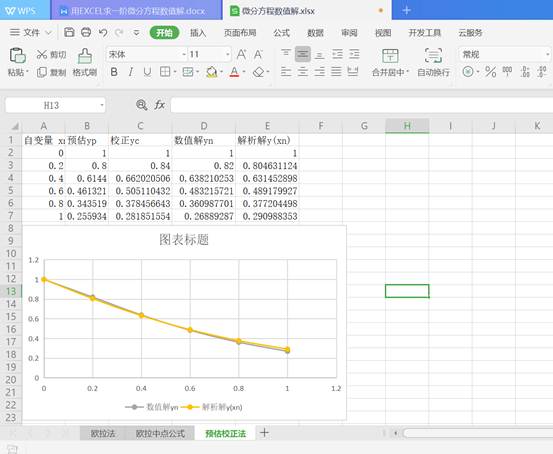
3.4 数值求解的改进欧法——预估校正法
类似的步骤,全部选中绘图,然后选中图形,删除yp,yc对应图形,可得下图,可见与欧拉法相比,图形得到改善,数值解与解析解比较接近。
还剩下龙格库塔法,小朋友们,自己试一试吧。
王福昌编写 2018-12-01
